삽입 정렬
삽입 정렬
이미 정렬되어 있는 서브 리스트에 새로운 원소를 추가하는 방식입니다. 비교 원소는 데이터를 한 칸씩 뒤(오른쪽)로 밀면서 삽입할 위치를 찾습니다. 해당 정렬 방식은 삽입 위치를 찾는 과정과 삽입을 위한 공간을 마련하는 과정이 동시에 진행됩니다.
원리
⓵ 인덱스 0번 원소는 이미 정렬이 완료된 원소 입니다. 따라서 인덱스 1번부터 정렬을 시작합니다.
⓶ 자신의 앞(i-1) 인덱스부터 0번 인덱스까지 비교를 진행합니다.
⓷ 해당 인덱스에 들어있는 원소가 현재 인덱스에 들어있는 원소보다 크면 자리를 바꿉니다.
⓸ 더이상 현재 인덱스 원소보다 큰 값이 없다면 자리를 찾은 것입니다.
⓹ 해당 인덱스에 현재 인덱스 원소를 넣습니다.
⓺ 그 다음 인덱스의 정렬을 시작합니다.
*정렬할 원소가 없을 때까지 반복
자신의 앞 인덱스들과 비교를 진행하는 이유는 현재 인덱스 앞 원소들은 이미 정렬이 완료된 것이라고 보기 때문입니다. 이미 정렬이 완료된 배열에 현재 인덱스 값을 삽입한다고 생각하면 삽입 정렬을 이해하기 쉬울겁니다.
예시
삽입 정렬을 그림으로 나타내봤습니다. 주어진 배열 [9, 7, 2, 13, 10] 를 삽입 정렬을 사용해서 정렬해보겠습니다.
비교할 원소 중에 pivot 값보다 큰 값이 있으면 뒤로 밀려나고 pivot이 자리를 잡으면 그 다음 pivot 으로 옮겨서 같은 방식으로 정렬을 진행합니다.
 InsertionSort.swift
InsertionSort.swift
저는 삽입 정렬 코드를 이렇게 구현해봤습니다. 밑에서 자세하게 설명해보겠습니다.
func insertionSort(arr: [Int]) {
var arr = arr
for i in 1..<arr.count {
var pivotIndex = i
let pivot = arr[i]
for j in stride(from: i-1, through: 0, by: -1) where arr[j] > pivot {
arr[j+1] = arr[j]
pivotIndex = j
}
arr[pivotIndex] = pivot
}
}
Swift
복사
⓵ 0 인덱스는 이미 정렬이 되어 있다고 가정했기 때문에 1번 인덱스부터 마지막 인덱스까지 정렬을 진행할 겁니다. ⓶ 먼저 현재 index를 pivotIndex에 저장해줍니다. pivotIndex는 다음 for문에 들어가게 되면 j 인덱스를 저장해줄 것이고, 아니라면 현재 index를 return해줄겁니다. ⓷ 그 다음 pivot 값을 저장해줍니다. pivot은 현재 인덱스에 들어있는 값으로 다음 for문에서 대소 비교를 할 때, 이동한 위치에 값을 넣을 때 사용될 겁니다.
⓸ 이제 현재 인덱스 앞에 있는 인덱스(i-1)부터 대소 비교를 진행합니다. where 절에 따라 현재 값이 pivot에 들어있는 값보다 크다면 코드 블럭 안으로 들어가서 ⓹ 값을 뒤로 미는 코드를 실행합니다. 그리고 ⓺ 해당 인덱스를 pivotIndex에 저장합니다. pivot 보다 작은 값이 나타나면 for문을 멈추고 ⓻ 현재 인덱스에 pivot 값을 넣어줍니다.
for i in 1..<arr.count { // ⓵
var pivotIndex = i // ⓶
let pivot = arr[i] // ⓷
for j in stride(from: i-1, through: 0, by: -1) where arr[j] > pivot { // ⓸
arr[j+1] = arr[j] // ⓹
pivotIndex = j // ⓺
}
arr[pivotIndex] = pivot // ⓻
}
Swift
복사
 시간 복잡도
시간 복잡도
삽입 정렬의 시간 복잡도는 최선과 최악의 상황에서 차이가 납니다.
func insertionSort(arr: [Int]) {
var arr = arr
for i in 1..<arr.count { // ⓵
var pivotIndex = i
let pivot = arr[i]
for j in stride(from: i-1, through: 0, by: -1) where arr[j] > pivot { // ⓶
arr[j+1] = arr[j]
pivotIndex = j
}
arr[pivotIndex] = pivot
}
}
Swift
복사
최선의 상황일 경우,
⓵ 1부터 n까지 원소를 한 개씩 탐색하기 때문에,
⓶ 이미 정렬이 되어 있기 때문에 where 절 조건을 만족하지 못해서,
● 결론적으로, 가 걸리게 됩니다. 효율적인 정렬 알고리즘은 병합 정렬 보다 빠른 속도입니다.
최선의 상황에서는 이미 정렬이 완벽하게 되어 있습니다. 해당 상황에서는 where 절의 arr[j] > pivot 조건을 만족하지 못해서 다음 for문에 들어가지 않습니다.
최악의 상황일 경우,
⓵ 1부터 n까지 원소를 한 개씩 탐색하기 때문에,
⓶ where 절 조건도 만족하고 stride도 알차게 돌아서 0 인덱스까지 탐색하기 때문에,
● 결론적으로, 가 걸리게 됩니다. 앞서 봤던 선택 정렬, 버블 정렬과 동일한 속도를 가집니다.
삽입 정렬은 선택, 버블 정렬과는 다르게 최악과 최선의 시간차이가 많이 날 것 같습니다. 성능을 확인하기 위해서, 저는 10000부터 1까지 거꾸로 들어있는 배열과 정렬이 완벽하게 되어 있는 배열, 두 개를 각각 넣어보려고 합니다.
var arr: [Int] = []
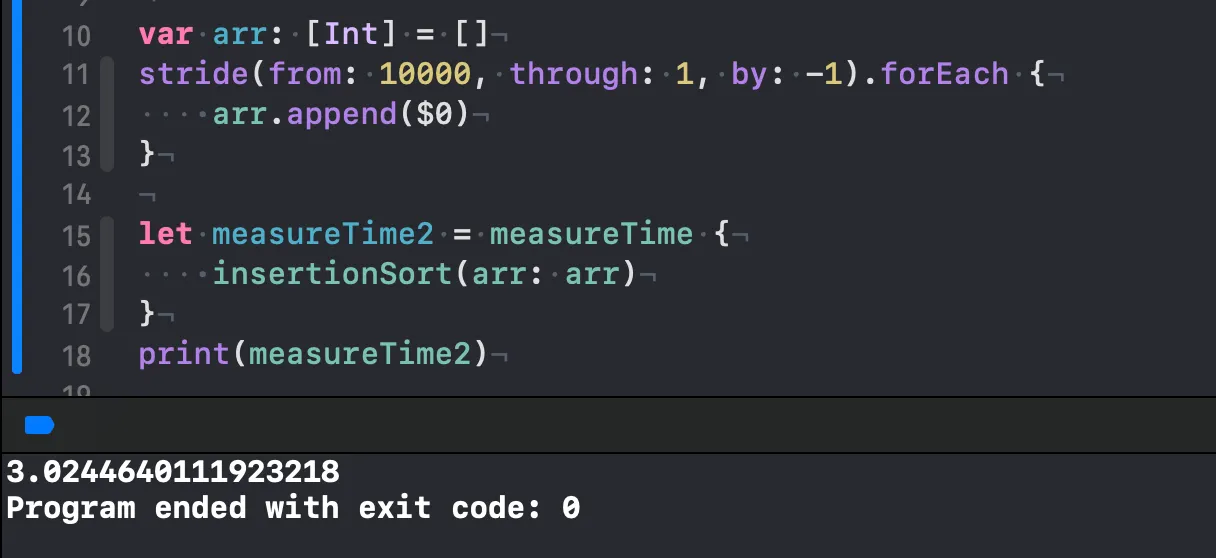
stride(from: 10000, through: 1, by: -1).forEach {
arr.append($0)
}
Swift
복사
var arr: [Int] = []
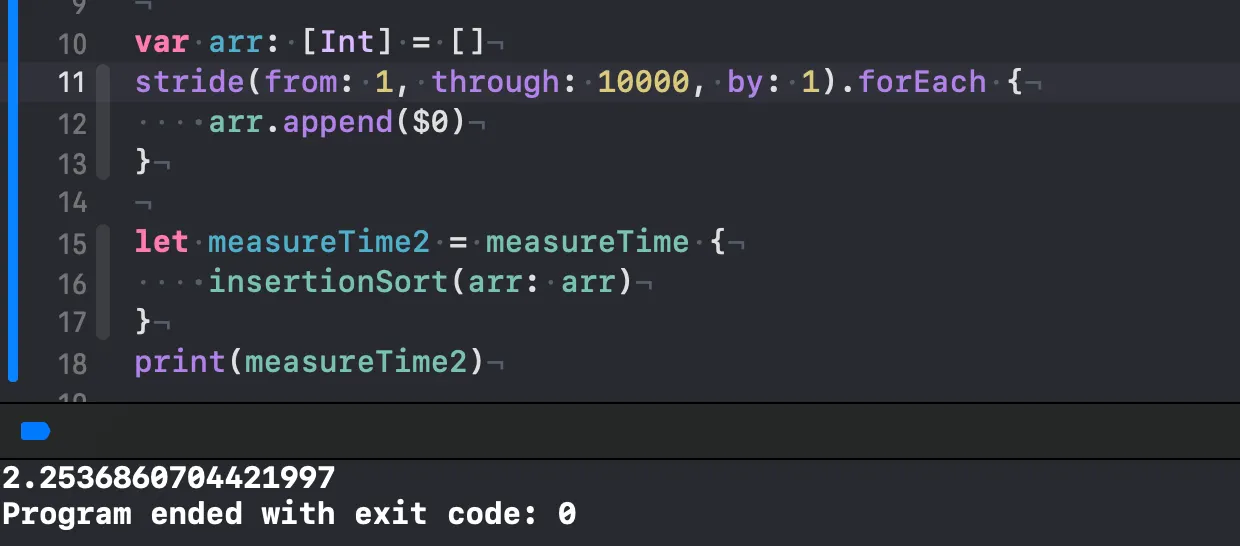
stride(from: 1, through: 10000, by: 1).forEach {
arr.append($0)
}
Swift
복사
그리고 삽입 정렬을 사용해서 정렬을 진행했습니다.
•
삽입 정렬(최선)
•
삽입 정렬(최악)
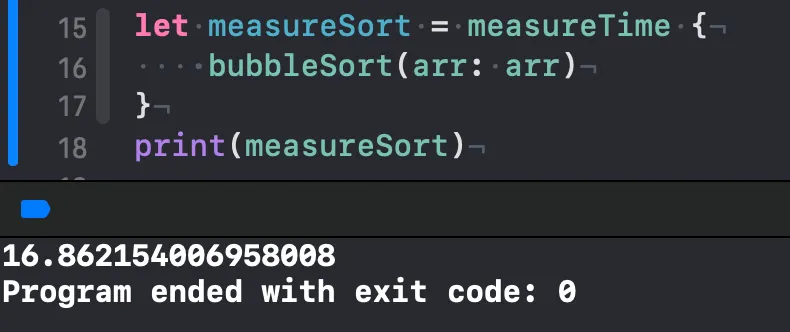
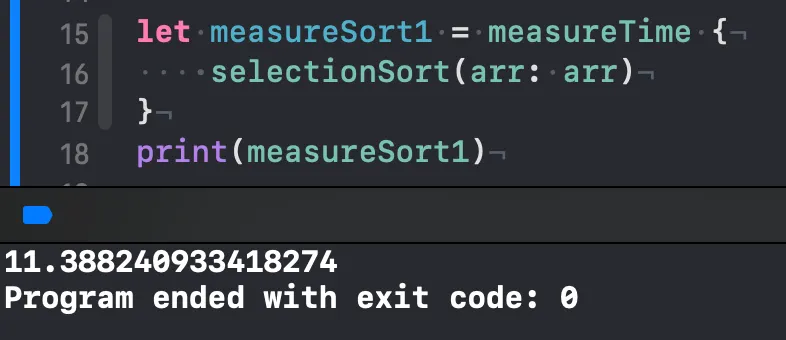
놀랍게도 10000개의 원소가 들어있는 배열에선 최악과 최선이 얼마 차이가 안나네요. 그리고 버블 정렬, 선택 정렬보다 빠릅니다. 거의 8-13초정도 빠릅니다. 이전에 했던 결과들도 보여드리겠습니다.
•
•
•
sort()
그래도 아직 sort() 메서드를 이기는 건 없네요..
 +⍺
+⍺
점점 시간이 당겨지는 걸 보니 효율적인 알고리즘들은 얼만큼의 속도를 낼 지 기대가 됩니다.
코드는 깃허브에 올려뒀습니다!