힙 정렬
힙 정렬
힙 정렬은 이진 트리의 한 종류인 최대 힙을 이용한 정렬 방식입니다. 최대 힙은 각 노드의 키 값이 그 자식 노드보다 크거나 같은 최대 트리 조건을 만족하는 이진 트리를 말합니다. 모든 노드의 부모 노드가 자식 노드의 값보다 크기 때문에 루트값(트리 가장 상위)에는 트리에 있는 모든 원소 중에 가장 큰 값이 위치하게 됩니다.
이 특성을 이용해서 가장 큰 값을 찾아내어 그 값을 제외한 후에 정렬되는 과정을 반복하는 방식입니다.
원리
⓵ n개의 요소를 최대힙이 되도록 구성합니다.
⓶ 최대힙이 되면 루트값을 맨 뒤의 요소와 바꿉니다.
⓷ 맨 뒤의 요소를 제외한 나머지 부분에서 루트값을 찾습니다.
⓸ 해당 루트값을 이전 루트값 앞에 위치한 요소와 바꿉니다.
*최대힙에 요소가 하나만 남을때까지 반복
먼저, 배열 전체를 최대힙 상태로 만든 후에 루트 값을 하나씩 뒤로 빼면서 뒤에서부터 정렬이 되도록 하는 방식입니다.
그런데, 배열을 어떻게 최대힙 상태로 만들 수 있나요?
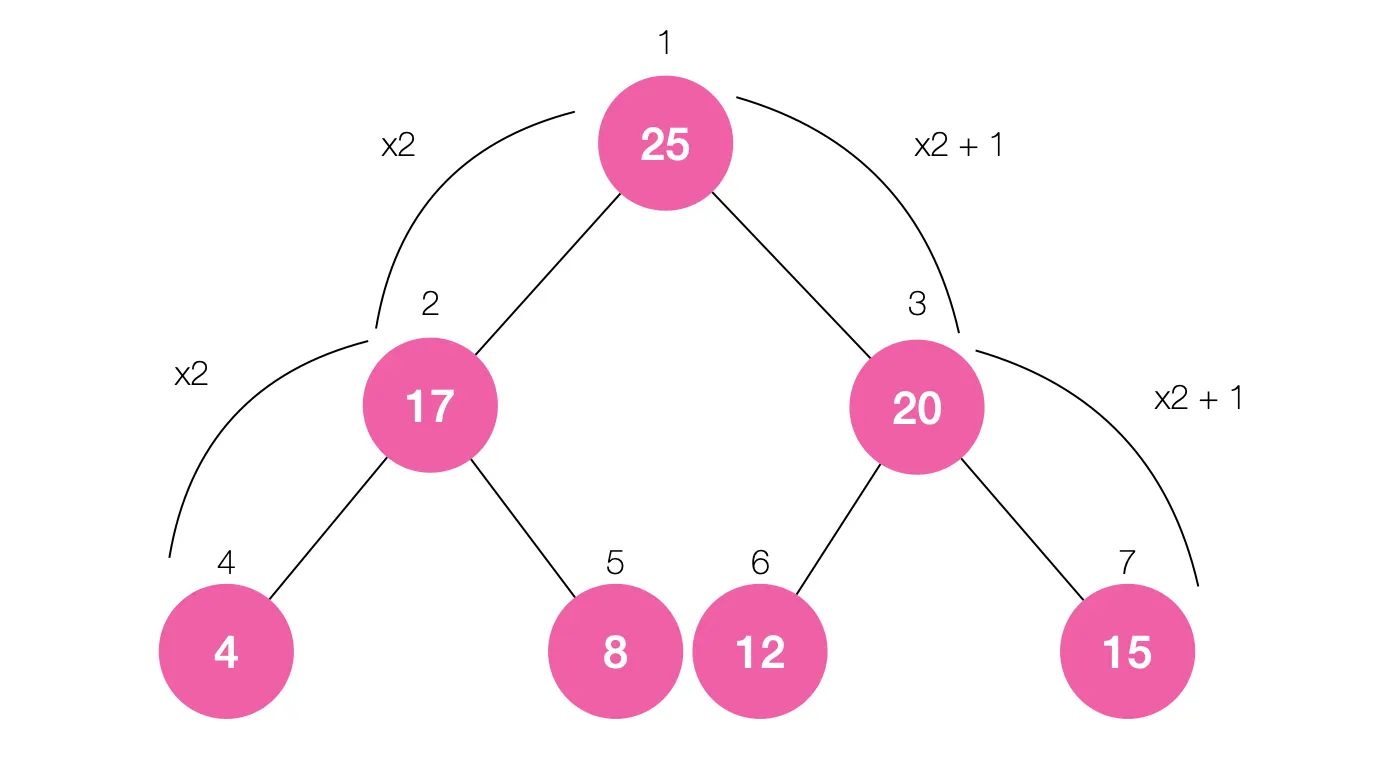
이진 트리는 하단의 그림처럼 생겼습니다. 각 노드마다 위에서 차례대로 1번부터 N번까지 부여한다고 해볼게요.
그러면, 그림에 있는 규칙을 발견할 수 있습니다.
자식 노드는 부모 노드가 가지는 숫자 인덱스에 x2, x2+1한 값을 인덱스로 가집니다. 해당 규칙을 참고해서 현재 인덱스의 x2, x2+1한 노드의 값이 현재 노드의 값보다 큰 지, 작은 지를 확인해주면 됩니다.
예시
힙 정렬을 영상으로 나타내봤습니다. 힙 정렬은 다른 정렬 방식들과는 다르게 조금 복잡한 부분들이 있어서 ⓵ 최대힙을 구성하는 부분과 ⓶ 루트값을 계속 뒤로 위치시키는 부분을 따로 영상으로 만들었습니다.
주어진 배열 [24, 7, 80, 3, 64, 15, 50, 10, 42, 18]를 힙 정렬을 사용해서 정렬해봤습니다.
일단, 최대힙 구성을 시작하는 부분은 전체 N 중에 /2한 부분에 해당하는 N/2 인덱스부터 시작할겁니다.
위에서 설명한 공식대로라면 맨 마지막 노드에 /2한 부분까지만 부모 노드가 있기 때문에 그 이후에 있는 노드에는 자식 노드가 없어서 자식 노드가 현재 노드보다 큰 지, 작은 지 확인할 필요가 없습니다.
이제 루트값을 맨 뒤로 보내고 맨 뒤에 있는 값을 앞으로 보내서 위에서 진행한 루트값을 다시 찾는 작업을 반복적으로 진행할겁니다.
이전에 최대힙을 구성하면서 진행했던 방식을 동일하게 반복하면서 루트값을 찾고 그 값을 뒤로 보내어 정렬을 완료합니다.
 HeapSort.swift
HeapSort.swift
힙 정렬 코드를 이렇게 구현해봤습니다.
먼저, heapSort 함수는 최대힙을 구성하고, 구성한 최대힙을 가지고 루트값을 뒤로 보내면서 다시 최대힙을 구성하면서 정렬하는 코드를 담고 있습니다.
func heapSort(_ list: [Int], n: Int) -> [Int] {
var tempArr = list
for i in stride(from: n / 2, to: 0, by: -1) { // ⓵
makeHeap(&tempArr, index: i, n: n) // ⓶
}
for i in stride(from: n - 1, to: 0, by: -1) { // ⓷
let temp = tempArr[1] // ⓸
tempArr[1] = tempArr[i + 1]
tempArr[i + 1] = temp
makeHeap(&tempArr, index: 1, n: i) // ⓹
}
return tempArr
}
Swift
복사
일단, 자식 노드가 있는 부모 노드 위치부터 시작하기 위해서 ⓵ n / 2 위치부터 1까지 for문을 돌리면서 ⓶ 최대힙을 구성합니다.
최대힙을 구성하고 나면, ⓸ 최대힙을 맨 뒤로 보내고 맨 뒤에 있던 값을 루트로 보내어 ⓹ 최대힙을 다시 구성합니다. 최대힙을 다시 구성하면 새로운 루트값이 만들어지게 됩니다. 그 값을 반복적으로 뒤로 보내는 작업을 진행합니다. 이 작업은 ⓷ n - 1부터 1까지 이진 트리의 전체 노드 개수를 줄이면서 진행합니다.
이번엔 최대힙을 구성하는 코드를 볼게요.
func makeHeap(_ list: inout [Int], index: Int, n: Int) {
let temp = list[index] // ⓵
var child = index * 2 // ⓶
while child <= n { // ⓷
if child < n && list[child] < list[child + 1] { child += 1 } // ⓸
if temp > list[child] { break } // ⓹
else {
list[child / 2] = list[child] // ⓺
child *= 2 // ⓻
}
}
list[child / 2] = temp // ⓼
}
Swift
복사
먼저, ⓵ 현재 들어온 인덱스에 들어있는 값을 기준 값으로 잡습니다. 그리고, 해당 인덱스의 ⓶ 자식 노드에 해당하는 인덱스를 child 변수에 저장합니다. 이제 ⓷ child 인덱스가 전체 노드의 수보다 커지기 전까지 while 문을 돌면서 자식 노드와 부모 노드 내부의 값을 변경해줄겁니다.
가장 첫 번째로 확인해야 하는 것은 ⓸ 현재 자식 노드가 자신의 형제 노드보다 큰 값을 가지고 있는지 확인하는 겁니다. 형제 노드보다 큰 값을 가졌다면 해당 노드를 부모와 비교하면 되고, 아니라면 형제 노드를 비교하기 위해서 child 값에 1를 더해줍니다.
이제 비교할 자식 노드를 확인했으니, ⓹ 해당 자식 노드가 현재 부모 노드보다 큰 지 확인합니다. 만약, 부모 노드가 더 큰 값을 가지고 있다면, 자리를 바꿀 필요가 없기 때문에 그대로 while 문에서 나갑니다. 반대로, 자식 노드가 더 큰 값을 가지고 있다면, ⓺ 부모 자리에 해당 자식 노드 값을 위치시킵니다. 그리고, 해당 자식 노드의 자식 노드를 확인해보기 위해서 child의 레벨을 한 단계 낮춥니다.
해당 자식 노드의 자식 노드에서도 동일한 방식을 반복하면서 현재 부모 노드보다 크다면 자리를 바꿔주는 작업을 진행합니다.
⓼ while문 내부에서 모든 작업이 끝나고 나면 child의 현재 인덱스는 원래 가지고 있던 인덱스던지, 자신의 자식 노드의 인덱스를 가지고 있을 겁니다. 부모 노드의 값을 해당 인덱스의 /2한 부분에 넣습니다.
 시간 복잡도
시간 복잡도
힙 정렬의 시간 복잡도를 알아보기 위해서 heapSort를 보겠습니다.
func heapSort(_ list: [Int], n: Int) -> [Int] {
var tempArr = list
for i in stride(from: n / 2, to: 0, by: -1) { // ⓵
makeHeap(&tempArr, index: i, n: n)
}
for i in stride(from: n - 1, to: 0, by: -1) { // ⓶
let temp = tempArr[1]
tempArr[1] = tempArr[i + 1]
tempArr[i + 1] = temp
makeHeap(&tempArr, index: 1, n: i)
}
return tempArr
}
Swift
복사
heapSort 함수 내부를 보면 n / 2 번의 루프를 도는 for문과 n - 1 번의 루프를 도는 for문을 볼 수 있습니다. 이렇게만 보면, 의 시간 복잡도를 가지는 거 같지만, 내부에 makeHeap을 가지고 있기 때문에 해당 함수가 어느정도의 시간 복잡도를 가지는지를 알아야 합니다.
func makeHeap(_ list: inout [Int], index: Int, n: Int) {
let temp = list[index]
var child = index * 2
while child <= n { // ⓵
if child < n && list[child] < list[child + 1] { child += 1 }
if temp > list[child] { break }
else {
list[child / 2] = list[child]
child *= 2
}
}
list[child / 2] = temp
}
Swift
복사
makeHeap 함수 내부에서 도는 while문을 보면 합병 정렬, 퀵 정렬과 마찬가지로 몇 단계에 걸쳐서 노드 비교가 진행됩니다. 현재 노드 개수가 10개라면 최대 3단계의 비교가 일어납니다. 즉, 만큼의 시간복잡도가 듭니다.
● 결론적으로, 이 걸리게 됩니다.
10000개의 원소가 들어있는 배열을 정렬할 때에 어느정도의 시간복잡도가 드는지 확인해보겠습니다.
•
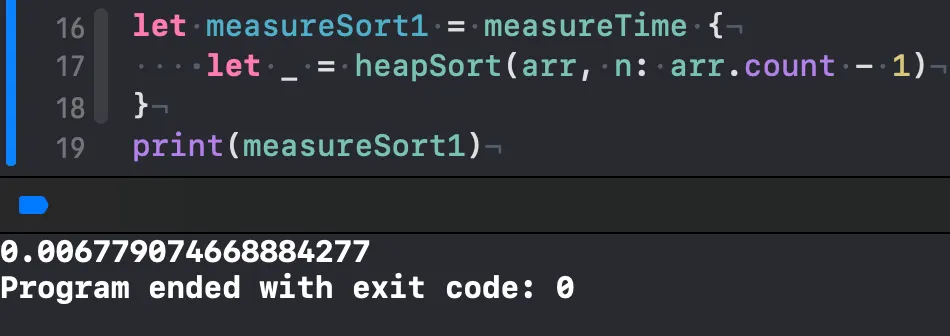
힙 정렬(정렬된 상태)
•
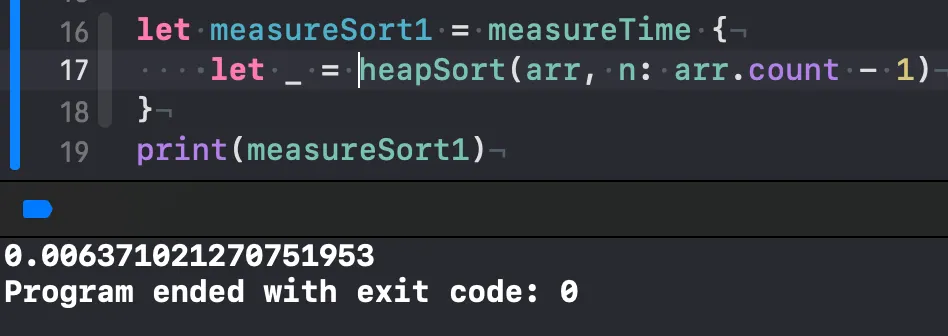
힙 정렬(거꾸로 정렬된 상태)
이전에 사용해봤던 합병 정렬, 신속 정렬보다도 빠르게 정렬되는 걸 볼 수 있습니다. ♡ ٩(´▽`)۶ ♡
 +⍺
+⍺
힙 정렬 관련 코드는 깃허브에 올려뒀습니다.