합병 정렬
합병 정렬
합병 정렬은 분할 정복(divide and conquer)이라는 알고리즘 디자인 기법에 근거하여 만들어진 정렬 방식입니다. 문제를 분할하고(divide) 분할된 문제를 해결(conquer)한 후에 해결 결과를 결합(combine)하는 형식으로 정렬이 진행됩니다.
원리
⓵ 리스트의 중간(mid)부분을 기점으로 2개의 서브리스트로 분할합니다.
⓶ 서브리스트 안에서도 중간(mid)부분을 기점으로 2개의 서브리스트로 분할합니다.
⓷ 서브리스트의 분할이 불가능해질 때까지 분할합니다.(재귀)
⓸ 모든 서브리스트들이 분할하지 못하는 상태가 되면, 이웃되는 요소들끼리 정렬하면서 병합합니다.
⓹ 모든 요소들이 하나의 리스트로 합쳐지면 정렬이 완료됩니다.
모든 리스트를 한 개의 요소만 가진 서브리스트가 될 때까지 나누고 해당 서브리스트를 이웃되는 요소들끼리 정렬하면서 합치는 방식입니다.
예시
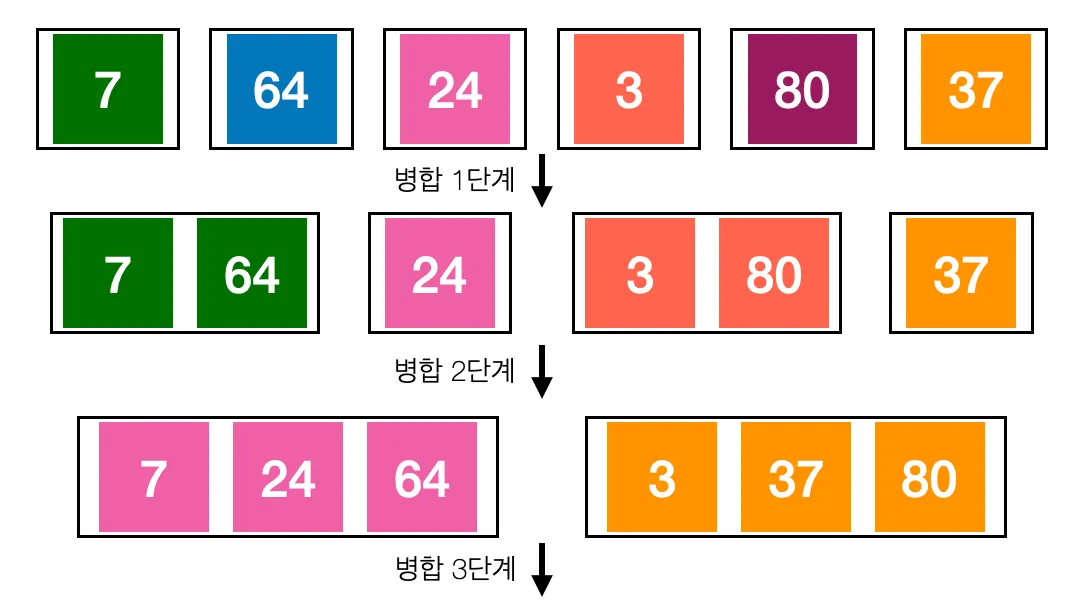
합병 정렬을 그림으로 나타내봤습니다. 주어진 배열 [7, 64, 24, 3, 80, 37]를 합병 정렬을 사용해서 정렬해볼게요.
전체적인 배열을 완벽하게 분해한 후에, 정렬을 하면서 다시 합치는 모습을 볼 수 있습니다.
 MergeSort.swift
MergeSort.swift
저는 합병 정렬 코드를 이렇게 구현해봤습니다. 자세하게 설명해볼게요.
먼저, 합병 정렬의 분할 부분을 구현한 mergeSort 함수입니다.
func mergeSort(_ list: [Int]) -> [Int] {
if list.count < 2 { return list }
let mid = list.count / 2 // ⓵
return merge(leftList: mergeSort(Array(list[0..<mid])), // ⓶
rightList: mergeSort(Array(list[mid..<list.count]))) // ⓷
}
Swift
복사
⓵ 분할을 하기 위해서 가운데 인덱스를 찾습니다. 그리고 merge 함수로 분할된 left 리스트와 right 리스트를 보내요. merge에서 어떤 작업을 하는지는 그 다음에 설명드릴게요. left 리스트는 ⓶ 첫번째 인덱스부터 가운데 인덱스 전까지, right 리스트는 ⓷ 가운데 인덱스부터 마지막 인덱스까지의 요소를 리스트 항목으로 가집니다.
mergeSort에 처음으로 들어간 리스트는 [7, 64, 24] / [3, 80, 37] 형태로 쪼개졌을 겁니다. 그리고 재귀적으로 mergeSort함수를 호출하면서 점점 더 잘개 쪼개져서 [7] / [64] / [24] / [3] / [80] / [37] 로 분할됐을 겁니다.
그러면, 이제 분할된 부분을 하나로 병합해서 정렬하는 코드를 확인해봅시다.
merge 함수는 mergeSort에서 left, right 리스트로 분할한 부분들을 가지고 정렬을 진행합니다.
func merge(leftList: [Int], rightList: [Int]) -> [Int] {
var lt = 0, rt = 0 // ⓵
var temp: [Int] = [] // ⓵
while lt < leftList.count && rt < rightList.count { // ⓶
if leftList[lt] < rightList[rt] { // ⓷
temp.append(leftList[lt])
lt += 1
} else { // ⓸
temp.append(rightList[rt])
rt += 1
}
}
temp += leftList[lt..<leftList.count] // ⓹
temp += rightList[rt..<rightList.count] // ⓹
return temp
}
Swift
복사
merge함수에서는 leftList와 rightList의 요소들을 하나씩 보면서 작은 값부터 임시 배열에다가 저장합니다. 분할된 서브리스트들은 정렬된 상태로 들어오기 때문에 결국 정렬된 상태로 저장되게 됩니다.
⓵ leftList와 rightList 배열에서 요소의 위치를 가르키는 lt, rt 변수를 만들어주고, 임시로 값을 저장하는 temp 배열도 만들어줍니다. ⓶ lt나 rt가 각 배열 끝에 도달하기 전까지 while 루프를 돌도록 합시다. 하나라도 배열 끝에 도달하면 더이상 요소 비교가 불가능하기 때문에 while 루프를 멈출거예요.
⓷ leftList의 값과 rightList의 값을 비교했을 때, rightList의 값이 더 크다면 작은 값부터 임시 배열에 들어가야 하기 때문에 leftList의 값을 배열에 넣어주고 leftList의 요소 위치를 가르키는 lt 변수를 1 올려줍니다. 다음 요소를 비교해야 하니깐요. ⓸ 반대의 상황이라면 rightList의 값을 넣어주고 rt 변수를 1 올려주면 됩니다.
만약, leftList, rightList 둘 중 하나의 배열이라도 비교할 요소가 남아있지 않다면 while 문을 멈추고 ⓹ 남은 요소값들을 temp로 넣어줍니다. lt, rt가 배열 끝에 도달한 상태라면 빈 배열이 넘어갈겁니다. 아니라면 남은 값들이 temp로 넣어지겠죠? 위에서 말했지만 이미 정렬된 상태로 서브리스트가 들어오기 때문에 남은 값을 그대로 넣어줘도 정렬된 상태로 추가가 됩니다.
 시간 복잡도
시간 복잡도
병합 정렬의 시간 복잡도를 알아보기 위해서 merge함수를 보겠습니다.
func merge(leftList: [Int], rightList: [Int]) -> [Int] {
var lt = 0, rt = 0
var temp: [Int] = []
while lt < leftList.count && rt < rightList.count {
if leftList[lt] < rightList[rt] { // ⓵
temp.append(leftList[lt])
lt += 1
} else {
temp.append(rightList[rt])
rt += 1
}
}
temp += leftList[lt..<leftList.count]
temp += rightList[rt..<rightList.count]
return temp
}
Swift
복사
while문 내부에서는 ⓵ 비교 연산이 진행되고 있습니다.
모든 서브리스트가 분할할 수 없는 상태라면 [7] / [64] / [24] / [3] / [80] / [37] 상태일겁니다.
맨 처음으로 들어오는 서브리스트는 아마 [7] / [64] 일겁니다. 그리고 while문 내부에서 1번의 비교연산이 진행됩니다. 그리고, temp 배열로 남은 값들을 보내기 위해 해당 리스트가 비었는지 비교하는 비교 연산이 1회 더 진행됐을 겁니다. 그렇게 생각하면, [7] / [64]를 병합하는데 드는 비교연산은 2회입니다.
그러면, [7] / [64] / [24] / [3] / [80] / [37]를 병합 1단계에서 비교 연산을 한 횟수는 최대 4회가 됩니다.
병합 2단계에서 [7, 64] / [24]에 드는 비교 연산 횟수는 어떻게 될까요?
while문 내부에서 2번의 비교 연산이 진행됩니다. 그리고 남은 배열을 넣기 전에 비었는지 확인하는 비교 연산이 1회 더 진행됐다고 생각하겠습니다. 그렇게 생각하면, [7, 64] / [24]를 병합하는데 드는 비교연산은 3회입니다.
그러면, [7, 64] / [24] / [3, 80] / [37]를 병합 2단계에서 비교 연산을 한 횟수는 최대 6회가 됩니다.
병합 3단계에서 [7, 24, 64] / [3, 37, 80]에 드는 비교 연산 횟수도 구해봅시다.
while문 내부에서 5번의 비교 연산이 진행됩니다. 그리고 남은 배열을 넣기 전에 비었는지 확인하는 비교 연산이 1회 더 진행됐다고 생각하겠습니다. 그렇게 생각하면, [7, 24, 64] / [3, 37, 80]를 병합하는데 드는 비교연산은 6회입니다.
그러면, [7, 24, 64] / [3, 37, 80]를 병합 3단계에서 비교 연산을 한 횟수는 최대 6회가 됩니다.
이를 통해서, 정렬의 대상인 데이터의 수가 n개일 때, 병합 정렬에서 진행되는 최대 비교연산의 횟수가 최대 n번 이라는걸 알 수 있습니다.
근데, 각 n번의 비교연산이 몇 번 진행되었을까요?
비교연산이 몇 번 진행되었는지, 알아야지만 횟수를 알 수 있습니다.
정렬 대상이 6개라고 할 때, 총 3번의 병합 단계를 거치게 됩니다. 즉, 만큼의 단계를 거치게 됩니다.
● 결론적으로, 이 걸리게 됩니다.
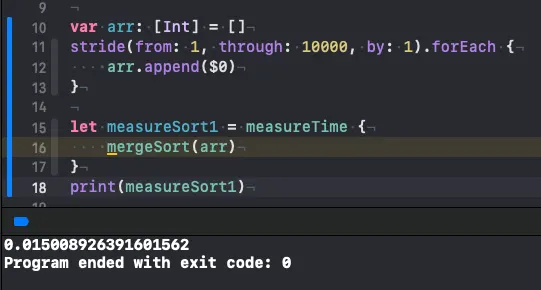
10000개의 원소가 들어있는 배열을 정렬할때에 어느정도의 시간복잡도가 드는지 확인해보겠습니다.
•
병합 정렬(정렬된 상태)
•
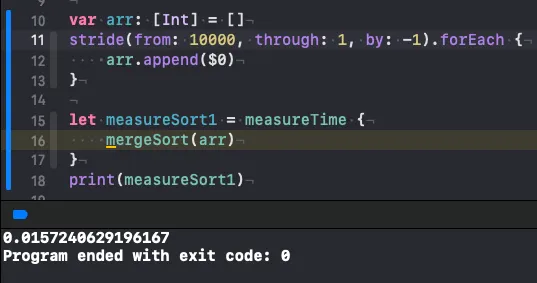
병합 정렬(거꾸로 정렬된 상태)
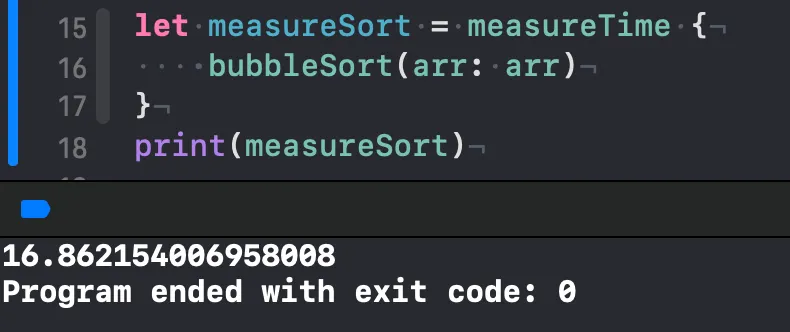
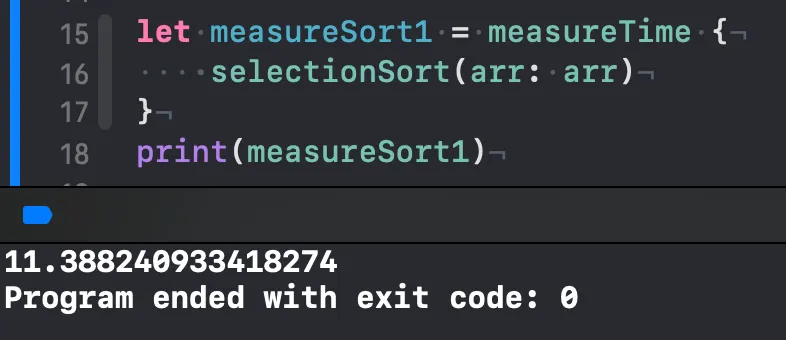
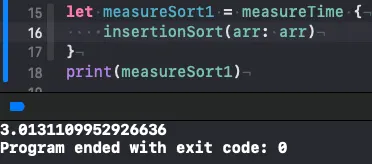
이전에 작성했던 삽입, 버블, 선택 정렬보다 훨씬 빨라졌습니다.
•
•
•
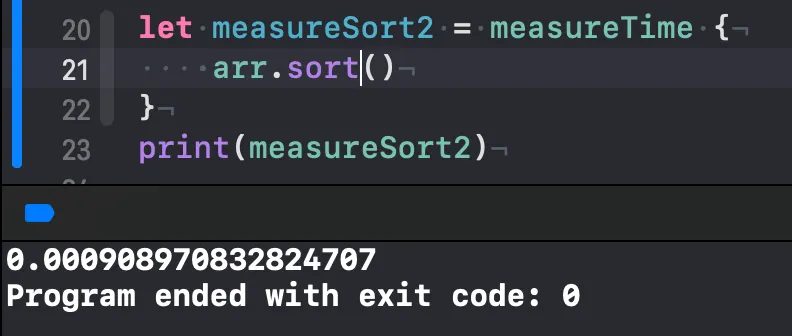
물론, 아직도 sort함수가 제일 빠릅니다.
 +⍺
+⍺
다른 효율적인 알고리즘들도 얼른 확인해봐야겠네요.
코드는 깃허브에 올려뒀습니다!